IECG Theory
Integral Equation Coarse-Graining Method
The IECG method is a theoretical approach to coarse-grain polymer liquids, based on the solution of the Ornstein-Zernike integral equation theory.[1] At the atomistic level the IECG relies on the PRISM approach by Schweizer and Curro[2], which is an extension to polymeric liquids of the RISM approach by Chandler and Andersen.[3] In the IECG Ornstein-Zernike equation, atomistic sites are described as real sites and coarse-grained sites are described as artificial sites, so that the radial distribution function (RDF) of the CG sites is expressed as a function of the RDF of the atomistic sites.[4],[5] A hypernetted chain closure connects the IECG potential to the RDF of the IECG sites.
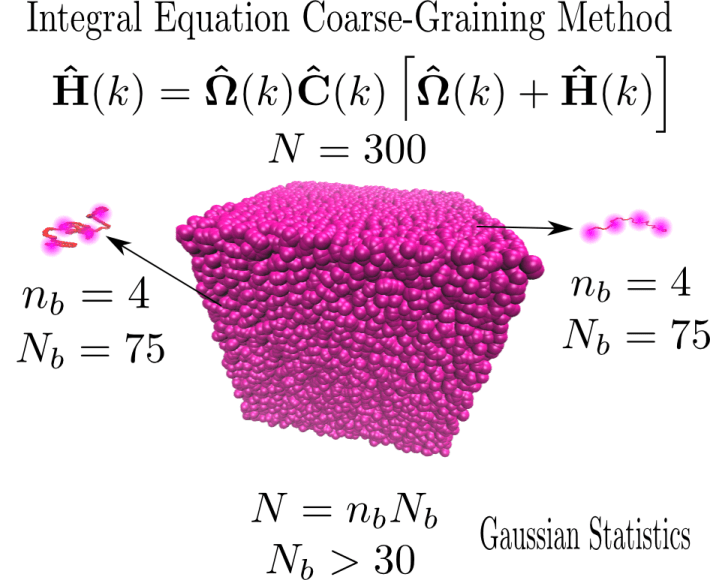
Figure 1. Illustration of polymer chains represented by four blobs (nb=4), where each chain consists of 300 monomers (N=300), and the number of monomers in each blob is large enough to allow one to use the Gaussian statistics to obtain the intramolecular correlation functions between blob and monomer,![]() bm(k), and between monomer and monomer,
bm(k), and between monomer and monomer,![]() mm(k). These functions enter the IECG-OZ equation at the bottom of the figure, where h̑mm(k) is the monomer-monomer intermolecular total distribution function, defined in real space as the radial distribution function menus one, hmm(r)=gmm(r)-1.
mm(k). These functions enter the IECG-OZ equation at the bottom of the figure, where h̑mm(k) is the monomer-monomer intermolecular total distribution function, defined in real space as the radial distribution function menus one, hmm(r)=gmm(r)-1.
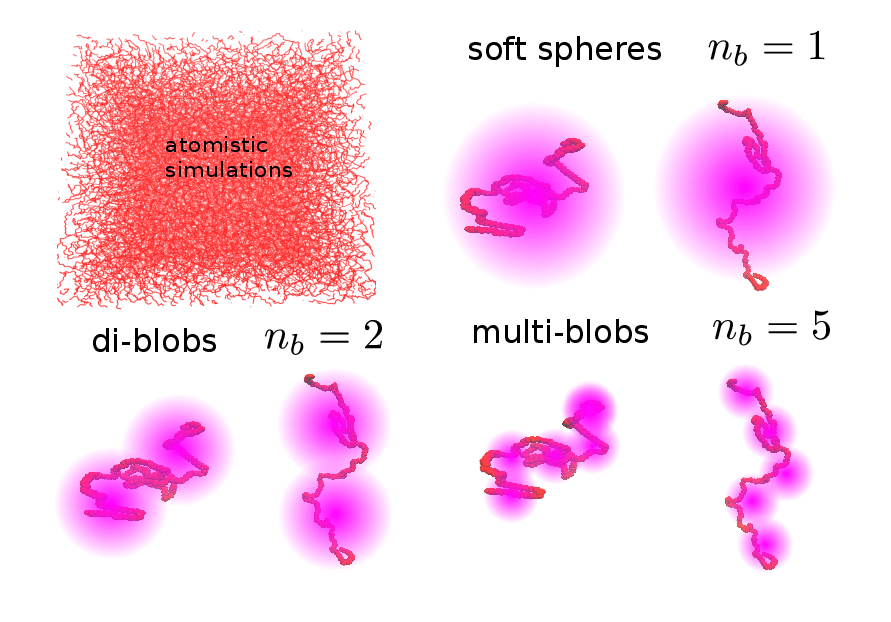
Figure 2. Examples of various coarse-grained granularities in the IECG model.
In the IECG model, each polymer in the melt is described as a chain of CG units, positioned at a distance along the chain comparable to or larger than the persistence length. As shown in the Figure each polymer is partitioned into a number, nb, of blobs or CG units. In the case where nb = 1, the polymer is described as a point particle interacting with a soft potential, i.e., the soft sphere model. In soft sphere or multi-blob representations, each blob represents a number of monomers, Nb, such that the total number of monomers in a chain is N = nbNb.
The IECG-OZ equation is then solved as
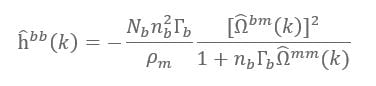
where Γb = —Nb ρm c0 and c0 is the monomer-monomer direct correlation function at k=0. From the IECG-OZ equation, one derives the blob-blob direct correlation function as
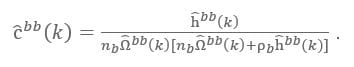
The IECG potential between coarse-grained sites is calculated using the HNC closure equation from the Fourier transform of the previous equations as
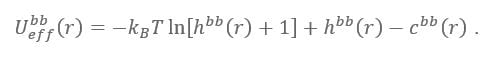
While atomistic MD simulations provide useful information in the temporal trajectory of the space and momentum coordinates, from which all the structural, thermodynamics, and dynamic quantities can be calculated, they are limited to the range of length- and timescales that they can cover when simulating polymeric liquids, and rarely reach the conditions typically sampled experimentally. On the other hand, the PRISM approach has no significant limitations in the range of length-scales that it can cover, and has been validated for a wide number of polymeric systems, but it provides information only at the level of the pair distribution functions, and their Fourier transforms, analogous to a scattering experiment. Thus, the IECG method addresses a much-needed niche in the study of complex polymeric liquids, because it connects the flexibility and accuracy of the PRISM theory to the convenient representation of the temporal evolution of the system through space coordinate and velocity trajectories. And, when combined with atomistic simulations in a multiscale procedure, the IECG simulations provide detailed information on a wide range of time- and length-scales.[6]
The advantages of the IECG method are that:
- Accuracy: the IECG simulations predict pressure and radial distribution functions in quantitative agreement with atomistic simulations performed at the same thermodynamic conditions. Because the pressure is consistent between coarse–grained and atomistic simulations performed at the same thermodynamic conditions, every thermodynamic quantity that can be formally derived from the pressure is also consistent. For example, we observe consistent excess free energy between IECG and atomistic simulations, with the advantage of the considerable speed up of the IECG simulations with respect to the atomistic ones.
- Transferability: because the IECG potential has been solved analytically for polymer melts, it is applicable to different polymeric systems, and can be applied to the same system at different thermodynamic conditions once the temperature and density dependence of the direct correlation function at wavevector k=0 (c0) is known.
- Computational efficiency: the IECG method has a net computational gain of several orders of magnitude, depending on the length of the polymer chain, the number of polymers in the simulation box, and the thermodynamic conditions.[7]
[1] Hansen, J. P., McDonald, I. R. (2003). Theory of Simple Liquids. Academic Press, Amsterdam.
[2] Schweizer, K., Curro, J. (1994). PRISM Theory of the Structure, Thermodynamics, and Phase Transitions of Polymer Liquids and Alloys. Advances in Polymer Science, 116, 319 – 377. https://doi.org/10.1007/BFb0080203
[3] Chandler, D., Andersen, H. C. (1972). Optimized Cluster Expansions for Classical Fluids. II. Theory of Molecular Liquids. J. Chem. Phys., 57 (5), 1930–1937. https://doi.org/10.1063/1.1678513
[4] Clark, A. J., McCarty, J., Lyubimov, I. Y., Guenza, M. G. (2012) Thermodynamic Consistency in Variable-Level Coarse Graining of Polymeric Liquids. Physical Review Letters, 109 (16). https://doi.org/10.1103/PhysRevLett.109.168301
[5] Dinpajooh, M., Guenza, M. G. (2018). On the Density Dependence of the Integral Equation Coarse-Graining Effective Potential. J. Phys. Chem B, 122, 3426–3440. https://doi.org/10.1021/acs.jpcb.7b10494
[6] Guenza, M. G., Dinpajooh, M., McCarty, J., Lyubimov, I. Y. (2018). Accuracy, Transferability, and Efficiency of Coarse-Grained Models of Molecular Liquids. J. Phys. Chem. B, 122 (45), 10257–10278. https://doi.org/10.1021/acs.jpcb.8b06687
[7] Dinpajooh, M., Guenza, M. G. (2018). Coarse-Graining Simulation Approaches for Polymer Melts: The Effect of Potential Range on Computational Efficiency. Soft Matter, 14, 2018, 7126–7144. https://doi.org/10.1039/C8SM00868J